SUCESIONES DE CÓNICAS
Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.
Perspectiva de las secciones cónicas.
Las cuatro secciones cónicas en el plano.
En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:
β < α : Hipérbola (naranja)
β = α : Parábola (azulado)
β > α : Elipse (verde)
β = 90º: Circunferencia (un caso particular de elipse) (rojo)
Y β= 180º : Triangular
Si el plano pasa por el vértice del cono, se puede comprobar que:
Cuando β > α la intersección es un único punto (el vértice).
Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice.
Cuando β = 90º El ángulo formado por las rectas irá aumentando a medida β disminuye,cuando el plano contenga al eje del cono (β = 0).
Expresión algebraica[editar]
Partiendo de una circunferencia (e=0), al aumentar la excentricidad se obtienen elipses, parábolas e hipérbolas.
En coordenadas cartesianas, las cónicas se expresan en forma algebraica mediante ecuaciones cuadráticas de dos variables (x,y) de la forma:
en la que, en función de los valores de los parámetros, se tendrá:
h² > ab: hipérbola.
h² = ab: parábola.
h² < ab: elipse.
a = b y h = 0: circunferencia.
a:C y Z:0:Triangular
Mediante un software se pueden representar las gráficas de la ecuación general de las cónicas. A continuación se presentan los tres casos: Parábola, elipse e hipérbola.
LA CIRCUNFERENCIA
La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro. Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro en una cantidad constante que se denomina radio.
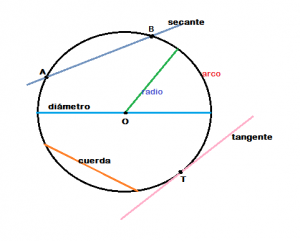
ELEMENTOS DE LA CIRCUNFERENCIA
ELEMENTOS DE LA CIRCUNFERENCIA
La circunferencia tiene una serie de elementos característicos, entre los que podemos destacar:
- Radio: es el segmento de recta que une O con cualquiera de los puntos del borde.
- Cuerda: segmento que une dos puntos cualquiera de la circunferencia.
- Diámetro: es el trazo que corresponde a la cuerda más grande que se puede dibujar en la circunferencia. Esta pasa por O, y su longitud corresponde a la de dos radios.
- Tangente: es una recta que intersecta a la circunferencia en exactamente un punto. A este punto le llamaremos punto de tangencia.
- Secante: es la recta que intersecta en dos puntos a la circunferencia.
- Arco: es una porción de la circunferencia determinada por dos puntos distintos de ella.
ECUACIONES DE LA CIRCUNFERENCIA
ECUACIONES DE LA CIRCUNFERENCIA
¿Qué es una circunferencia?
De manera formal, una circunferencia se define como el lugar geométrico de los puntos del plano equidistantes de otro, llamado centro de la circunferencia.
No debemos nunca confundir el concepto de círculo con el concepto de circunferencia, que en realidad una circunferencia es la curva que encierra a un círculo (la circunferencia es una curva, el círculo una superficie).
A continuación vemos una imagen de una circunferencia.
En realidad, y de manera más sencilla, una circunferencia es el conjunto de puntos situados en el plano todos a la misma distancia de un mismo punto central, al que llamaremos centro, y del que hablaremos más adelante con detalle en la parte de elementos básicos de la circunferencia.
Dados las coordenadas del centro de la circunferencia C(h;k) y el radio "r" de la misma, podemos utilizar la siguiente ecuación para determinar el valor de "y" correspondiente a un valor de "x".
Ejemplo:
Hallar la ecuación de la circunferencia cuyo centro es C(2;6) y con radio r = 4
(x - 2)² + (y - 6)² = 4²
Ecuación Canónica de la Circunferencia
Sean ahora las coordenadas del centro de la circunferencia C(0;0) y el radio "r", podemos utilizar la siguiente ecuación para determinar el valor de "y" correspondiente a un valor de "x".
Ejemplo:
Hallar la ecuación de la circunferencia cuyo centro es el origen y con radio r = 3
x ² + y ² = 3²
La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro (recordar que estamos hablando del Plano Cartesiano y es respecto a éste que trabajamos).
Determinación de una circunferencia
 |
Una circunferencia queda determinada cuando conocemos:
Tres puntos de la misma, equidistantes del centro.
El centro y el radio.
El centro y un punto en ella.
El centro y una recta tangente a la circunferencia.
También podemos decir que la circunferencia es la línea formada por todos los puntos que están a la misma distancia de otro punto, llamado centro .
Esta propiedad es la clave para hallar la expresión analítica de una circunferencia (la ecuación de la circunferencia ).
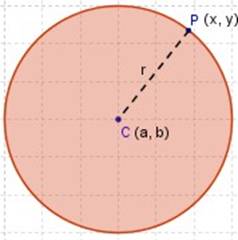
Entonces, entrando en el terreno de la Geometría Analítica , (dentro del Plano Cartesiano ) diremos que ─para cualquier punto, P (x, y) , de una circunferencia cuyo centro es el punto C (a, b) y con radio r ─, la ecuación ordinaria es
(x ─ a) 2 + (y ─ b) 2 = r 2
¿Qué significa esto?
En el contexto de la Geometría Analítica significa que una circunferencia graficada con un centro definido (coordenadas) en el Plano Cartesiano y con radio conocido la podemos “ver” como gráfico y también la podemos “transformar” o expresar como una ecuación matemática.
Así la vemos
|
Así podemos expresarla
|
 |
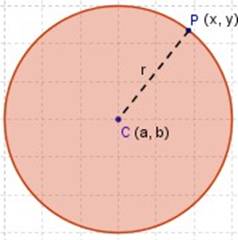Donde:
(d) Distancia CP = r
y
Fórmula que elevada al cuadrado nos da
(x ─ a) 2 + (y ─ b) 2 = r 2
También se usa como
(x ─ h) 2 + (y ─ k) 2 = r 2
|
Recordar siempre que en esta fórmula la x y la y serán las coordenadas de cualquier punto (P) sobre la circunferencia, equidistante del centro un radio (r) . Y que la a y la b (o la h y la k , según se use) corresponderán a las coordenadas del centro de la circunferencia C(a, b) .
Nota importante:
Los ejercicios sobre esta materia pueden hacerse en uno u otro sentido.
Es decir, si nos dan la ecuación de una circunferencia , a partir de ella podemos encontrar las coordenadas de su centro y el valor de su radio para graficarla o dibujarla.
Y si nos dan las coordenadas del centro de una circunferencia y el radio o datos para encontrarlo, podemos llegar a la ecuación de la misma circunferencia.
Cuadrado del binomio
Aquí haremos una pausa para recordar el cuadrado del binomio ya que es muy importante para lo que sigue:
El binomio al cuadrado de la forma (a ─ b) 2 podemos desarrollarlo como (a ─ b) (a ─ b) o convertirlo en un trinomio de la forma a 2 ─ 2ab + b 2 .
|
Sigamos nuestro razonamiento sobre la ecuación (x ─ a) 2 + (y ─ b) 2 = r 2 (que en forma matemática representa una circunferencia).
De la ecuación ordinaria a la ecuación general
Si en esta ecuación ordinaria ─cuyo primer miembro (lado izquierdo) está formado por la suma de dos cuadrados de binomio─, eliminamos los paréntesis desarrollando dichos binomios, pasamos todos los términos al primer miembro y la igualamos a cero, tendremos:
x 2 ─ 2ax + a 2 + y 2 ─ 2by + b 2 ─ r 2 = 0 ecuación que ordenada sería
x 2 + y 2 ─ 2ax ─ 2by + a 2 + b 2 ─ r 2 = 0
ECUACIÓN CANÓNICA DE LA ECLIPSE
Dada la ecuación reducida de la elipse 
,
,
hallar las coordenadas de los vértices de los focos y la excentricidad.
La ecuación de una elipse centrada en el origen y con focos en F(c, 0) y F'' (-c, 0) es
Demostración:
Sustituyendo en la fórmula de uno cualquiera de los radios vectores se obtiene:
Þ a2x2 + a2c2 + a2y2 = a4 + c2x2 Þ
Þ b2x2 + a2y2 = a2b2 Þ
