TERCER PERIODO

6 de julio del 2016

ÁNGULOS DE ELEVACIÓN Y DE PRECION 

ÁNGULO DE ELEVACIÓN: Es el ángulo que se forma entre la visual de un observador que mira hacia arriba y la horizontal

ÁNGULO DE DEPRESIÓN: Es el ángulo que se forma entre la visual de un observador que mira hacia abajo y la horizontal

ver dibujos.

Como se puede observar, en el dibujo de la izquierda, el ave observa hacia abajo al insecto y la horizontal esta a la altura de su vista, por lo tanto el angulo es de depresión. En el dibujo de la derecha el señor, sentado en su silla de ruedas, observa los globos "hacia arriba" por lo tanto el angulo es de elevación.

Para tener en cuenta: En ambos ángulos, la visual del observador será la hipotenusa del triángulo que se forma al plantear una situación problema de este tipo.

Ahora usted esta en capacidad de construir un dibujo con cada situación, diferentes a las presentadas arriba.

Ejemplos de aplicación:

NOTA. En la resolución de triángulos rectángulos vinos qué funciones y procesos utilizar de acuerdo a la información suministrada para su solución. En este tema se aplica la misma situación para resolver los interrogantes.

Ejemplo No 1

Un piloto de un barco observa al vigía de un faro con un ángulo de elevación de 32º. Si la altura del faro es de 135 m, calcular la distancia del faro al barco, y la visual del piloto.

(Una observación muy válida: si fuera el vigilante del faro el que observara al piloto del barco, entonces hablaríamos de angulo de depresión)

Solución.

Observemos la figura.

 

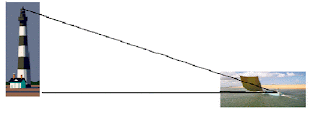
Se ha generado un triangulo rectángulo, recto en la base del faro. La visual del piloto es la hipotenusa, el ángulo de elevación está formado con la hipotenusa y la horizontal, Luego podemos construir un triangulo auxiliar donde ubicaremos a información suministrada, o si lo prefiere en el mismo dibujo.

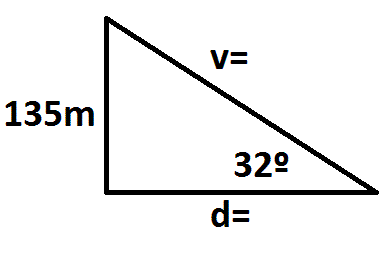
Hallamos d con la función tangente, ya que conocemos el cateto opuesto al ángulo de 32º  y vamos a buscar el cateto adyacente

Ahora calculamos la visual v (hipotenusa) con la función Seno de 32º

Ambos resultados, al trabajarlos directamente en la calculadora científica, ofrecen un poco de diferencia en los decimales.
Ejemplo 2.
Un electricista subido en un poste, observa a su ayudante que está en el piso a 25 metros del pie del poste, con un ángulo de depresión de 40º. Calcular la altura del poste.
Solución. Nótese cómo se elabora la gráfica cuando se trata de ángulo de depresión, el cual aparece fuera del triángulo que que se genera, pero es igual  al otro ángulo alterno interno
La información se muestra en la gráfica.

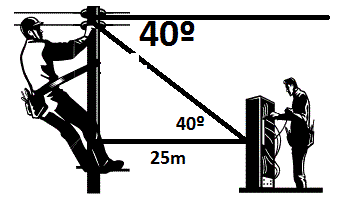
Observemos que el ángulo de depresión se trasladó al interior del triangulo
NOTA: Vemos así que el ángulo de elevación, siempre es igual al ángulo de depresión, y la visual es la hipotenusa.
Calculamos con tangente de 40º la altura h  del poste.

Usted está en capacidad de hallar la medida de la visual (v), es decir,  de la hipotenusa. Por favor use la función Coseno de 50º (La respuesta es 32,76 m)

EJERCICIOS

POBLEMAS SOBRE ÁNGULOS DE ELEVACIÓN Y DE DEPRESIÓN

IDENTIDADES TRIGONOMÉTRICAS

Identidades trigonométricas fundamentales

1Relación seno coseno

cos² α + sen² α = 1

2Relación secante tangente

sec² α = 1 + tg² α

3Relación cosecante cotangente

cosec² α = 1 + cotg² α

Ejemplos:

1 Sabiendo que tg α = 2, y que  180º < α <270°. Calcular las restantes razones trigonométricas del ángulo α.

2 Sabiendo que sen α = 3/5, y que  90º <α <180°. Calcular las restantes razones trigonométricas del ángulo α.

Razones trigonométricas de la suma y diferencia de ángulos

Ejemplos:

Razones trigonométricas del ángulo doble

Ejemplos:

Razones trigonométricas del ángulo mitad

Ejemplos:

Transformación de operaciones

1 Transformaciones de sumas en productos

Ejemplos:

2 Transformaciones de productos en sumas

Ejemplos:

Las identidades trigonométricas son ecuaciones que contienen funciones trigonométricas.

Razones trigonométricas

• Seno de α:
  
• Coseno de α:
  
• Tangente de α:
  

Razones trigonométricas inversas

Cosecante de α:

Secante de α:

Cotangente de α:

Relación entre razones trigonométricas

Nota: el signo ± que corresponde en cada caso depende del cuadrante en que esté el ángulo.

Relaciones trigonométricas básicas

• Identidad fundamental de la trigonometría
  
  
  
• Relación entre el seno, coseno y tangente
  
  
  
• Relación trigonométrica entre la tangente y la secante
  
  
  
• Relación trigonométrica entre la cosecante y la cotangente
  
  
  

Ángulos complementarios

• Seno del ángulo complementario:
  
  
  
• Coseno del ángulo complementario:
  
  
  
• Tangente del ángulo complementario:
  
  
  
• Cosecante del ángulo complementario:
  
  
  
• Secante del ángulo complementario:
  
  
  
• Cotangente del ángulo complementario:
  
  
  

Ángulos suplementarios

• Seno del ángulo suplementario:
  
  
  
• Coseno del ángulo suplementario:
  
  
  
• Tangente del ángulo suplementario:
  
  
  
• Cosecante del ángulo suplementario:
  
  
  
• Secante del ángulo suplementario:
  
  
  
• Cotangente del ángulo suplementario:
  
  
  

Ángulos conjugados

• Seno del ángulo conjugado:
  
  
  
• Coseno del ángulo conjugado:
  
  
  
• Tangente del ángulo conjugado:
  
  
  
• Cosecante del ángulo conjugado:
  
  
  
• Secante del ángulo conjugado:
  
  
  
• Cotangente del ángulo conjugado:
  
  
  

Ángulos opuestos

• Seno del ángulo opuesto:
  
  
  
• Coseno del ángulo opuesto:
  
  
  
• Tangente del ángulo opuesto:
  
  
  
• Cosecante del ángulo opuesto:
  
  
  
• Secante del ángulo opuesto:
  
  
  
• Cotangente del ángulo opuesto:
  
  
  

Ángulos que difieren 90º

• Seno del ángulo que difiere 90º:
  
  
  
• Coseno del ángulo que difiere 90º:
  
  
  
• Tangente del ángulo que difiere 90º:
  
  
  
• Cosecante del ángulo que difiere 90º:
  
  
  
• Secante del ángulo que difiere 90º:
  
  
  
• Cotangente del ángulo que difiere 90º:
  
  
  

Ángulos que difieren 180º

• Seno del ángulo que difiere 180º:
  
  
  
• Coseno del ángulo que difiere 180º:
  
  
  
• Tangente del ángulo que difiere 180º:
  
  
  
• Cosecante del ángulo que difiere 180º:
  
  
  
• Secante del ángulo que difiere 180º:
  
  
  
• Cotangente del ángulo que difiere 180º:
  
  
  

Transformaciones de razones trigonométricas

• Suma en producto
  
  
  
  
  
  
  
  
  
  
  
  
• Producto en suma
  
  
  
  
  
  
  
  
  
  
  
  

Razones trigonométricas del ángulo suma

• Seno del ángulo suma:
  
  
  
• Coseno del ángulo suma:
  
  
  
• Tangente del ángulo suma:
  
  
  

Razones trigonométricas del ángulo resta

• Seno del ángulo resta:
  
  
  
• Coseno del ángulo resta:
  
  
  
• Tangente del ángulo resta:
  
  
  

Razones trigonométricas del ángulo doble

• Seno del ángulo doble:
  
  
  
• Coseno del ángulo doble:
  
  
  
• Tangente del ángulo doble:
  
  
  

Razones trigonométricas del ángulo mitad

• Seno del ángulo mitad:
  
  
  
• Coseno del ángulo mitad:
  
  
  
• Tangente del ángulo mitad:
  
  
  

Razones trigonométricas del ángulo triple

• Seno del ángulo triple:
  
  
  
• Coseno del ángulo triple:
  
  
  
• Tangente del ángulo triple:
  
  
  

Teorema del seno

El teorema del seno relaciona proporcionalmente los lados y los ángulos de un triángulo. Éste enuncia que:

Cada costado de un triángulo (a, b y c) es directamente proporcional al seno del ángulo opuesto (A, B y C).

La razón entre un lado y el seno del ángulo opuesto es igual al diámetro (el doble del radio, 2R) de la circunferencia (L) en la que se circunscribe el triángulo.

Es decir, todas las razones entre cada lado (a, b y c) y el seno del ángulo opuesto (A, B y C) son directamente proporcionales y dicha proporción es 2R.

Teorema del coseno

El teorema del coseno relaciona un lado del triángulo con los otros dos y el ángulo que forman éstos. El teorema enuncia que:

El cuadrado de un lado (a, b o c) cualquiera de un triángulo es igual a la suma de los cuadrados de los dos lados restantesmenos el doble del producto de ellos por el coseno del ángulo (A, B o C) que forman.

El teorema del coseno es una generalización del teorema de Pitágoras para cualquier triángulo.

De hecho, si el ángulo A fuese recto (90º), su coseno seria cero, quedando: a² =  b²+c². Si el ángulo A fuese obtuso, es decir >90º, entonces el coseno sería negativo.

EJERCICIOS 

Comprobar las identidades trigonométricas:

1

2

3

4

5

6

7

Simplificar las fracciones:

1

2

3